В течение последних пяти лет в рамках Рождественских чтений проходит конференция на тему: «Наука в свете православного миропонимания». Мы попробуем  немного уточнить и даже усилить это название и спросить: что православный взгляд на мир, православный опыт может дать науке?

Достаточно распространено мнение, что наука и вера, православие, говорят о разном и потому не могут противоречить друг другу. Однако вся многовековая история противостояния и борьбы науки и религии свидетельствует, что ситуация здесь гораздо сложнее. Представление о коренном противоречии между наукой и религией, между научным и религиозным мировоззрениями проходит через всю европейскую историю Нового времени и достаточно широко распространено теперь. Попытки объявить это противоречие несуществующим или как-то его сгладить не приносят, по видимости, желаемого результата. Мне уже приходилось высказываться на эту тему[1], и моя точка зрения состоит в том, что без серьезной конкретнойработы никакого движения в этом вопросе не произойдет. Общие декларации не помогут ни в какой мере.

Именно поэтому я и хотел бы выяснить, что православный взгляд на мир, православный опыт может дать науке? Этот опыт велик и многообразен. В него входит духовный опыт Церкви, представленный личными молитвенными подвигами как прославленных подвижников Церкви, так и простых мирян. Он также воплощен в сложных и разветвленных богослужебных формах.

Нас будет интересовать богослужение как форма и структура духовного опыта Церкви. Поставленный общий вопрос можно сформулировать так: «Может ли изучение структуры православного богослужения как формы православного опыта дать что-то науке?»

I. Первый, самый поверхностный взгляд на строение богослужения показывает, что в его структуру входят циклы или круги. Прежде всего, оно состоит из трех кругов: дневного, седмичного и годового. Отдельно следует сказать о богослужении Вечности – Божественной Литургии. Приведем очень краткое описание, выделяя наиболее значимые моменты для сопоставления структур циклов в православии и естественных науках. Дневной круг начинается вечером и состоит из следующих служб:

Вечерня (18.00) строится в основном вокруг ветхозаветных сюжетов. В частности, вечерня начинается каждением храма в безмолвии (это действо символизирует Дух Божий ношашеся верху воды в прологе Творения, закрытие Царских врат – изгнание из рая).

Повечерие.

Полунощница (полночь).

Утреня (6 часов утра) содержит воспоминания о новозаветных событиях.

1-й час (начало дня, суд Пилата над Спасителем).

3-й час (9 часов утра, время сошествия Святого Духа на апостолов).

6-й час (12 часов дня, время Распятия).

9-й час (3 часа дня – время, когда Иисус предал Свой дух Богу на Кресте).

Заметим, что вечерня и утреня в точности соответствуют началу и концу дня, как это изображено в первой главе книги Бытия: «И бысть вечер, и бысть утро». Таким образом, библейское представление о творении мира весьма существенно входит в структуру богослужения каждого дня.

Вся последовательность дневных служб содержит неизменные части, которые служатся одинаковым образом каждый день, и такие части, которые принадлежат седмичному и годовому кругам. Выбор последних зависит от того, в какой день недели или месяца они служатся. Части седмичного цикла содержатся в Октоихе иимеют следующий смысл:

Воскресенье                               Воскресение Христово
Понедельник                               Небесные силы – ангелы
Вторник                                     Иоанн Креститель и пророки
Среда                                         Крест (покаянные воспоминания о предательстве Иуды)
Четверг                                     Апостолы и святители
Пятница                                    Крест (Распятие)
Суббота                                    Все святые и Богородица.

Наконец, службы годового (неподвижного и подвижного) круга находятся в Минее и Триоди.Каждый день богослужебного круга связан с воспоминанием о каком-то событии или лице Священной истории. Имеется ценностная иерархия событий Священной – ветхозаветной и последующей христианской – истории. Наиболее важные события входят во все круги богослужения. Приведем два примера.

Творение мира является уникальным событием всей Священной истории. Оно отмечается каждый год в Новолетие (индикт 1 сентября каждого года).

Кондак праздника звучит так:

«В вышних живый, Христе Царю,/ всех видимых и невидимых Творче и Зиждителю,/ Иже дни и нощи, времена и лета сотворивый,/ благослови ныне венец лета,/ соблюди и сохрани в мире/ град и люди Твоя, Многомилостиве».

Творению мира посвящен и первый день каждой седмицы. И, наконец, каждый день оно отмечается в начале вечерни. Соответствующие службы имеются в каждом из трех кругов. Можно сказать, что имеется три времени: дневное, седмичное и годичное, которые циклически повторяются – каждое со своим периодом. И события Священной истории представлены во всех этих временах.

Другой пример можно привести из Новозаветной истории. Ее центральное событие также представлено во всех трех кругах богослужения:

Распятие Спасителя
Великая Пятница Страстной седмицы
Пятница каждой седмицы
6-й час полдень

Если принять, что каждый круг представляет свое время, то можно рассмотреть их времена как независимые друг от друга. Тогда многие события Священной истории происходят в каждом из них и определяют тем самым связь кругов друг с другом. Конечно, времена кругов богослужения связаны еще и с астрономическим временем. Имеется чисто естественнонаучное соответствие между ними, которое можно изобразить следующим рисунком:

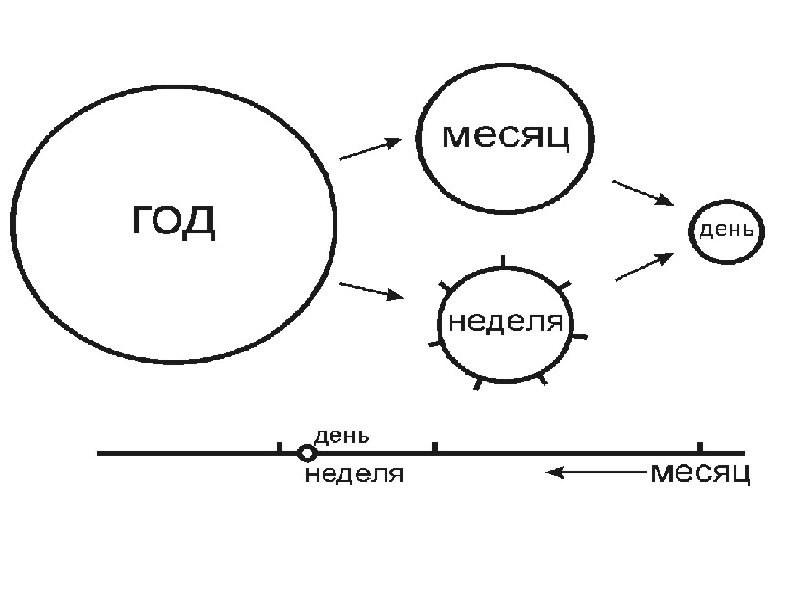  Рис. 1

Прямая внизу показывает, как времена кругов богослужения изображаются в линейном направленном времени.

Литургически время определяется своим содержанием – теми событиями, которые отмечаются, празднуются, поминаются в какой-то его момент. Если нечего поминать, то и времени просто нет. Итак, имеется соответствие кругов богослужения, которое определяется прежде всего праздниками и днями памяти, но при этом есть и астрономический аспект.

В православии можно увидеть и другие циклы (не только те, которые как будто имеют «естественнонаучное» происхождение). Это циклы Евангельских чтений и чтений других богослужебных книг. Рядовые чтения Евангелий на воскресных Литургиях, в которых тексты одного Евангелиста сменяются другими, состоят из трех циклов: а) от Пасхи до недели Пятидесятницы; б) от недели Всех Святых до недели о Закхее; в) от недели о мытаре и фарисее до Вербной недели.

Последовательное чтение рядовых Евангелий на Литургиях образует единую структуру со своим временем. В прилагаемом к богослужебному Евангелию указателе чтений прямо пишется, что «год в церковном исчислении времени, относительно (курсив авт.) чтения Евангелий и Апостола, начинается днем Светлого Христова Воскресения и разделяется на три круга».

Очевидно, что представление о времени каждого цикла или круга довольно явно выражено в богослужебной литературе. Кроме того, многие циклы не имеют никакого астрономического основания, и связи между ними устанавливаются только событиями Священной истории. Отсюда можно сделать вывод, что структура циклических времен, согласованных друг с другом, имеет не случайное или подсобное, но принципиальное значение в православном взгляде на мир. Можно сказать, что она имеет онтологическое значение и определяет строение православного мира.

II. Описанной нами циклической структурой времени далеко не исчерпываются представления о времени, имеющиеся в православии. Как было упомянуто выше, служба Божественной литургии не принадлежит ни одному из богослужебных кругов. Она находится вне них, как бы над ними и принадлежит вечности. Термин «вечность» используется в богослужебных текстах прежде всего применительно к векам или эонам. Они относятся к тварной вечности: тем самым признается, что сотворенный мир находится не только в историческом времени, но и в вечности.

Многие отцы Церкви писали, что «прежде» творения мира во времени было "некоторое состояние, приличное премирным силам, превысшее времени, вечное, присно продолжающееся"[2].

Ην τις πρεσοντέρα της του κόσμου γενέσεως κατάστασις ταις υπερκοσμίοις δυνάμεσι πρέπουσα, η υπέρχρονος, η αιωνία, η αίδιοσ.

Hom. In Hex. , 1, 5, 13A (SC 26bis)

Здесь речь идет именно о тварной, а не о божественной вечности. В ней и были созданы премирные силы, т. е. ангельский мир. Об этом же пишет и блаж. Иероним:

Sex milia necdum nostri orbis implentur anni et quantas prius aeternitates, quanta tempora, quantas saeculorum origines fuisse arbitrandum est in quibus angeli, throni, dominationes, ceteraeque uirtutes seruierint Deo, et absque temporum uicibus atque mensuris, Deo iubente, substiterint!

Hieronimus. Epist. ad Titum I77C (CCSL)

«Нашему миру не исполнилось и шести тысяч лет, сколько, должно полагать, до него протекло вечностей, сколько времен, сколько неизрéченных веков, в продолжение которых ангелы, престолы, власти и прочие силы служили Господу и существовали по воле Его, без всякого измерения и перемены времен» (перевод митр. Макария Булгакова).

В имеющейся литературе имеется явное невнимание к этому кругу вопросов[3]. И это несмотря на то, что упоминание Вечности происходит в богослужении практически не только в каждой службе, но и в каждой молитве! В завершении молитвы «Слава Отцу, и Сыну, и Духу Святому, и ныне, и присно, и во веки веков» имеющееся выражение «во веки веков» прямо относится к тварной, эонической вечности. Более того, здесь подчеркивается ее нетривиальная, иерархическая структура. Наиболее открыто об этом писал преп. Максим Исповедник в своих Главах, имеющихся в Добротолюбии (но, кажется, выпущенных в русском переводе свт. Феофана Затворника). Другим явным упоминанием тварной вечности является песнопение «и сотвори ему вечную память» в чине отпевания.

Если обратиться к философии таких церковных деятелей, как автор знаменитой «Церковной Истории» Евсевий, то он использует представление об эоне как бесконечной прямой. И циклические «конечные» эоны получаются из такой прямой выделением ограниченных отрезков и их сворачиванием[4].

В философии и науке представления о Вечности обширно использовались в Античности и в Средние века. Средневековой патристике предшествовала многовековая линия античного платонизма с детальной разработкой представлений об иерархии эонов у таких неоплатоников, как Плотин и Прокл. Но уже в философии и науке Нового времени совершилось полное изгнание каких-либо представлений о вечности. Характерно, что вечность отсутствует в философии времени Хайдеггера с ее онтологизацией текучего, исторического времени.

III. Следует перейти к рассмотрению времени в естествознании. В самых разных его отделах встречаются периодические процессы, которые используются для измерения времени. Их свойства можно формализовать в виде системы аксиом. Позже мы рассмотрим и  конкретные примеры.

Любое устройство или прибор для измерения времени, использующие какой-либо периодический процесс, называются часами. Таким образом, к часам относятся все виды периодических процессов, от колебаний электромагнитных волн и до движений небесных тел по орбитам. При отвлечении от конкретной физической структуры таких процессов и вводится неопределяемое понятие часов.

Аксиома 0. Время измеряется часами и только часами. Каждые часы имеют свой период и измеряют свой цикл (или свое время).

Аксиома 1. Часов (циклов) может быть сколь угодно много и все они согласованы (синхронизированы) друг с другом.

Аксиома 2. Существуют часы со сколь угодно большим периодом.

Аксиома 3. Существует минимальный период и периоды всех часов суть его целочисленные кратные[5].

Обсудим смысл этой аксиоматики. Прежде всего, можно предположить, что никаких других механизмов для измерения времени, кроме периодических процессов, не существует. Конечно, это может показаться слишком сильным утверждением. В природе имеется большое количество апериодических процессов, которые можно использовать для измерения времени. Например, распад атомного ядра. Но все такие процессы имеют начало и конец. Чтобы измерять время с их помощью сколь угодно долго, нужно их снова и снова «завести», а это вводит в процесс какой-то период. Простейший пример – песочные часы[6].

Математической идеализацией понятия часов является окружность, между точками которой имеется расстояние. Оно пропорционально углу, на который нужно повернуть окружность, чтобы перейти от одной точки к другой[7]. Полная длина всей окружности называется периодом часов.

Следующим основным понятием является синхронизациячасов. Наглядный пример – ручные часы, пока еще не исчезнувшие под напором дигитализации. Фактически это двое часов: одни (часовая стрелка) измеряют собственно часы, другие (минутная стрелка) измеряют минуты. Окружность, по которой стрелки движутся, нужно представить как две поначалу независимые окружности, которые в реальных часах соединены вместе.

Когда часовая стрелка проходит по (своей!) окружности ровно 1 час, минутная стрелка в это же время проходит полностью всю свою окружность.

Таким образом, взяв какой-то отрезок первой окружности (скажем, от 11 до 12 часов), каждой его точке можно сопоставить какую-то точку «минутной» окружности. При этом точкам «11 часов» и «12 часов» «часовой» окружности будет отвечать одна и та же точка «минутной» окружности. «Часовая» окружность состоит из двенадцати таких отрезков, и каждый из них можно таким способом отобразить на всю «минутную» окружность. Можно еще сказать, что «часовая» окружность двенадцать раз навивается на «минутную».

Вообще, если есть двое часов, окружностей, и одна из них (с большим периодом) навивается какое-то целое число раз на другую, то следует сказать, что часы (непосредственно) синхронизированы друг с другом. Наконец, если для пары часов найдутся такие третьи часы, что с ними будут непосредственно синхронизированы каждые из часов этой пары, то все они будут синхронизированы друг с другом. Необходимым условием синхронизации является простое соотношение: период одних часов является рациональным кратным периода других часов.

Аксиома 1 предполагает, что все имеющиеся часы могут быть синхронизированы друг с другом. Иначе можно сказать, что периоды всех часов соизмеримы друг с другом. По отношению к имеющимся в природе периодическим процессам это выглядит довольно сильным утверждением[8]. Заметим, однако, что имеющиеся измерения периодов не могут доказать несоизмеримость наблюдаемых физических величин. Они могут дать лишь какие-то аргументы в пользу такой несоизмеримости. Всегда можно сказать, что два изучаемых периода суть рациональные кратные какого-то очень малого числа, недоступного (пока) нашим наблюдениям. Ведь все физические приборы могут дать лишь рациональные числа в качестве результатов наблюдений.

Теперь обсудим Аксиому 2 о существовании часов со сколь угодно большим периодом. Если бы это было не так, то существовал бы некоторый верхний предел для измерения времени. Взяв часы с самым большим периодом и «живя» в их времени, наблюдатель имел бы повторяющееся время по истечении их периода. Такое можно предположить, если принять во внимание некоторые модели Вселенной, имеющиеся в общей теории относительности. Но в настоящее время, по видимому, не имеется окончательного суждения космологов о справедливости таких замкнутых (в частности, по времени) моделей. Кроме того, многие физические теории (например, классическая электродинамика) основаны на представлении о неограниченном четырехмерном физическом пространстве–времени (пространство Минковского, где пространственные и временные координаты не ограничены по величине).

Аксиома 3 наиболее спекулятивна. Невозможно представить каких-либо (квази-) физических аргументов в ее пользу. Единственный метафизический аргумент состоит в том, что каждая «настоящая» физическая теория имеет свою фундаментальную мировую константу (электродинамика – скорость света, кантовая теория – постоянную Планка и пр.) Единственный способ ввести в предлагаемую аксиоматику такую константу содержится в Аксиоме3. Отметим, что обсуждаемые далее следствия аксиом справедливы (с небольшими изменениями) и без Аксиомы 3 (и даже без Аксиомы 1). Принципиальный характер носят Аксиомы 0 и 2.

Итак, мы предполагаем, что имеется бесконечная иерархия часов, удовлетворяющих Аксиомам 0-3. Какие выводы о строении времени можно отсюда сделать?

Ньютон в своих «Математических началах натуральной философии» предположил, что имеется универсальное, равномерно текущее время, которым можно измерять все происходящее в природе. Это время можно представить в виде бесконечной прямой с евклидовым расстоянием на ней.

Любое событие в мире происходит в какой-то момент Универсального Времении, следовательно, определяет точку на этой прямой. Если взять какую-либо точку в качестве точки отсчета, то расстояние между этими точками отвечает на вопрос: когда произошло исходное событие?

В построенной нами системе часов моменты времени получаются как точки на окружностях. Никаких прямых мы не видим. Чтобы их получить, нужно использовать некоторые математические рассуждения.

В нашей картине часов много (бесконечно много!) и среди них есть (в силу Аксиом 1 и 2) бесконечная последовательность часов, в которой периоды следующих часов в два раза больше периода предыдущих. Период первых часов в последовательности пусть будет равен 1. Как отмечено выше, часы с большим периодом измеряют больший отрезок времени, и если требуется измерить «все» время бесконечной ньютоновской прямой, естественно брать часы со все большим периодом. И перейти к бесконечному пределу!

Как видно, в такой последовательности часов каждые следующие часы можно два раза навить на предыдущие. Чтобы получить универсальное время, не зависящее от выбираемых часов, нужно взять предел бесконечной последовательности циклических времен. Можно ли так получить бесконечную прямую? Да, легко. Разобьем прямую на отрезки длины 1. Тогда ее можно навить (бесконечное число раз) на окружность длины 1 (это первые часы из нашей последовательности). При этом бесконечно много точек прямой перейдут в одну и ту же точку окружности. Затем будем последовательно делить прямую на отрезки длины каждый раз в два раза больше и навивать на окружность (часы) с соответствующим периодом. Эти отображения (навивания) прямой на часы со все большими периодами будут согласованы друг с другом (в силу предложенной конструкции все часы последовательности синхронизированы), и кажется, что ньютоновская прямая будет пределом выбранной последовательности часов.

Этому пределу можно придать точный математический смысл (см. приложение) и определить Универсальное Время как предел по всем часам этой иерархии. Оказывается, что в этом пределе будет находиться и бесконечная прямая, изображающая универсальное ньютоновское время. Но (и это принципиальный вывод) таких прямых там будет бесконечно много (даже континуально много), и они ничем не будут отличаться друг от друга.

Таким образом, ньютоновское время получается в рамках предлагаемой системы, но оно теряет свою универсальность. Потеря универсальности времени происходит и в (специальной) теории относительности, но совсем по другим причинам и с другими последствиями. В нашей ситуации Универсальное Время представляет собой тугой пучок континуума бесконечно близких бесконечных прямых. Эта конструкция дает возможность соединить непротиворечиво систему циклических времен и линейное, направленное и бесконечно длящееся время.

IV. Как уже было сказано, время в православии составляется теми событиями, которые в нем отмечаются (поминаются). Похожая ситуация имеет место и в естествознании. Время существует не само по себе, а связано с происходящими в нем физическими (или иными) процессами. Мы говорили до сих пор о периодических процессах как измерителях времени, отвлекаясь от их физического (или иного) содержания. Следует обратиться к тому, как в природе проявляют себя такие периодические процессы, или, кратко, циклы. Можно сказать, что циклы в природе представляют собой механизм (или среду) для переноса материи и (или) информации. Хотелось бы сформулировать такие же общие свойства природных циклов, как это было сделано применительно к часам, абстрагируясь при этом от конкретных свойств физических, химических, биологических и иных процессов.

Можно начать с простого примера из жизни социума: путь человека на работу и обратно домой. В первом приближении его можно представить в виде движения по кругу «Дом → Работа → Дом», которое повторяется каждый день (если отвлечься от таких частностей, как выходные дни). Круг этот состоит (может состоять) из неизменно присутствующих в нем частей. Например, таких: «Дом → Станция метро 1 → Станция метро 2 → Работа → Станция метро 2 → Станция метро 1 → Дом».

Можно рассмотреть вместе соответствующие участки пути, а именно: «Дом → Станция метро 1 → Дом»; «Станция метро 1 → Станция метро 2 → Станция метро 1»;«Станция метро 2 → Работа → Станция метро 2»и объединить каждый из них в отдельный цикл. Здесь есть на вид разрывы (путь на станцию; туда утром, назад вечером). Поначалу такое объединение в единый цикл может показаться искусственным, но можно вспомнить структуру богослужения. Там идущие друг за другом службы всего богослужебного дня также принадлежат разным кругам: дневному, седмичному, годовому и другим, о которых мы также говорили выше.

Итак, помимо цикла хождения на работу, есть еще цикл хождения на станцию метро 1 из дома и назад, цикл поездки по линии метро от станции 1 до станции 2 и обратно и т.д. Можно сказать, что весь большой цикл состоит из таких трех циклов. Чтобы такая система переноса (в данном случае – людей на работу и обратно) могла работать, необходимо выполнение условий двух типов:

1) расписания движения по каждому циклу должны быть согласованы. Это значит, что времена (часы), определяемые каждым циклом, должны быть синхронизированы друг с другом;

2) каждый из циклов представляет собой путь для перемещения людей и имеет определенную пропускную способность. Нужно, чтобы в точках соединения путей выполнялись соотношения согласованности между количествами людей, проходящих в единицу времени. Эти соотношения можно сформулировать как законы сохранения (материи или информации).

Первое условие (синхронизация) относится ко Времени как таковому. Второе предполагает первое, но относится уже к «физике» процесса. Если оба эти условия выполнены, можно говорить о системе сопряженныхциклов.

Назовем рассмотренную ситуацию транспортной моделью[9] и предположим, что ее свойства являются наиболее общими свойствами циклов, имеющихся в природе.

Выше было сказано, что система часов может быть неограниченно расширена. Это же свойство отражено и в приведенной модели. Так, в цикл хождения на работу можно вставить, например, автобус от остановки (не)далеко от дома до станции метро и обратно. Менее очевидно, но ничем не хуже, путь от двери квартиры до входа в дом, даже шаг от одной ступеньки лестницы к другой вполне подходит.

Таким образом, наш исходной цикл включается в иерархию циклов, имеющую тенденцию к разрастанию. Правда рассматриваемый пример содержит включение в систему циклов со все меньшими периодами, в отличие от того, что было рассмотрено выше (можно предположить также наличие минимального периода). Это, впрочем, никак не противоречит приведенному выше предположению (когда-нибудь такое измельчение цикла хождения на работу может остановиться, достигнув какого-то естественного предела). С другой стороны, сам этот цикл, конечно же, включается в более обширные жизненные циклы человека, социума, биоценоза, биосферы и т.д.

Приведем несколько примеров природных циклов:

1. Углеродный цикл термоядерных реакций (цикл Бете –Вейцзеккера) (рис. 2)[10].

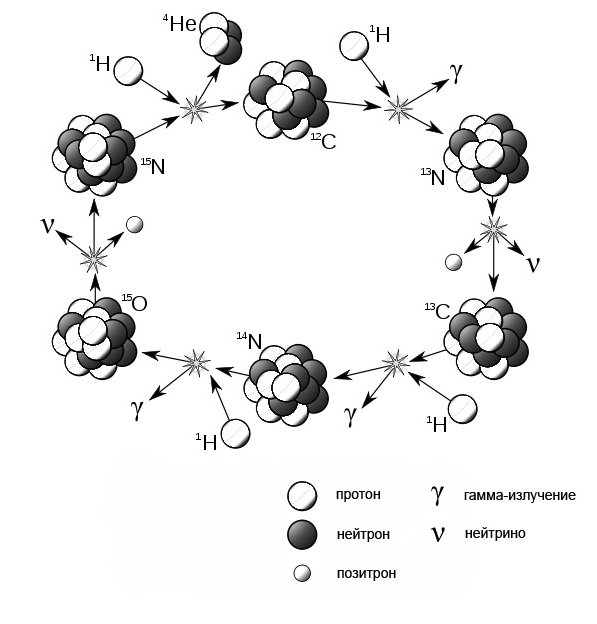
Рис. 2

2. Циклы в биосфере (вода, кислород, углерод, азот и другие элементы) (рис. 3).

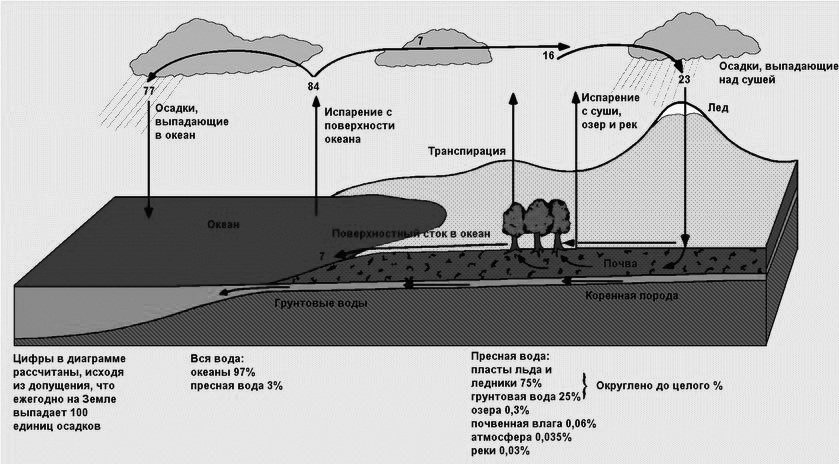
Рис. 3

3. Циклы в биоценозах (пример: отношения паразита и хозяина или симбионтов)[11].

4. Циклы в организме (перенос кислорода и углекислого газа эритроцитами крови).

5. Биохимические циклы метаболизма клетки: цикл Кребса[12] или цикл переноса электронов в митохондриях (дыхание) животных или пластидах (фотосинтез) растений (рис. 4).

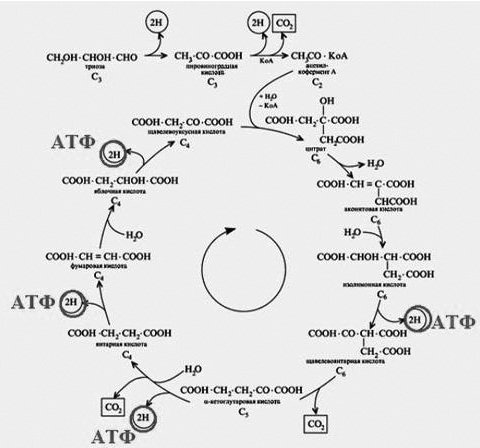
Рис. 4

Все приведенные нами примеры (и огромное множество других) не суть изолированные циклические процессы. Они связаны друг с другом самым тесным образом. Между ними есть многочисленные связи. Так, термоядерные реакции дают солнечный свет, являющийся исходным для процесса фотосинтеза растений. В процессе фотосинтеза растения поглощают углекислый газ и выделяют кислород, а животные – наоборот, поглощают кислород, сжигают его в митохондриях и выделяют углекислый газ. Отсюда можно сделать выводы:

1. Все имеющиеся в природе циклы взаимосвязаны и сопряжены друг с другом.
2. Эти связи могут быть прослежены от биохимических масштабов и до процессов, происходящих в космосе.

Нельзя со всей уверенностью утверждать, что все имеющееся изобилие природных (и социальных) циклов принадлежит такой единой системе[13], но в качестве вполне оправданного шага научной абстракции такое допущение можно (и нужно!) сделать[14].

Можно ли принять также, что в системе сопряженных циклов существуют циклы сколь угодно большого периода, т.е. система циклов допускает потенциальное расширение до бесконечности?

V. Иерархии в православии и биологии .Предполагаемыенами бесконечные системы часов и циклов имеют иерархический (соподчиненный) характер. Приведем еще аргументы совсем другого типа в пользу их (потенциальной) бесконечности. Иерархии циклов можно и нужно сравнить с линейными иерархиями, связанными с симметриями переноса.

Иерархичность пронизывает всю жизнь православия: существуют Иерархия небесная бесплотных небесных ангелов и иерархия церковная, представляющая собой структуру земной Церкви. Ее очень четкое изображение можно увидеть во многих храмах (например, на столпах Успенского собора московского Кремля; рис. 5).

Рис. 5

Здесь ясно видна геометрическая линейная структура, связанная с иерархией святых. Она, очевидно, конечна, и возникает вопрос о ее потенциальной бесконечности. Поскольку земная иерархия представляет собой в некотором смысле отражение небесной, то для нас немаловажен вопрос о бесконечности именно небесной иерархии. Он обсуждался в богословии: рассматривалась даже явная (актуальная) бесконечность ангельской иерархии (митр. Макарий Булгаков, о. Павел Флоренский)[15]. Такая возможность допускалась в качестве частного мнения.

Обратимся теперь к примерам из биологии, из морфологии растений и животных. Линейные периодические структуры у растенийвесьма распространены. Вот пример (фотография Карла Блоссфельда) (рис. 6)[16]:

Рис. 6

Можно предположить, что подобная структура имеет тенденцию к бесконечному росту, и все имеющиеся сегменты растения стремятся стать одинаковыми. Более того, предположим, что имеется идеальная структура, к которой стремится растение. Такой структурой является бесконечная прямая, разделенная на отрезки равной длины. По самому смыслу растения, его основная «задача» – неограниченный рост, в реальном мире сдерживаемый условиями окружающей среды, питанием и просто физикой нашего пространства. Можно допустить наличие идеального архетипа (данного) растения, гетевское Urpflanze , который не просто является образцом, а который существует в некотором идеальном умопостигаемом пространстве.

Каждое растение должно иметь свой идеальный бесконечный образ, и оно растет одновременно в нем и в нашем (декартовом) физическом пространстве[17].

Точнее, растение, развиваясь, увеличивается одновременно и в физическом пространстве, и в пространстве идеального бесконечного дерева. Основное свойство любого растения – не только потенциально бесконечный рост, но и потенциальная способность к бесконечному ветвлению[18].

Аналогичные построения (хотя и с меньшей легкостью) неоднократно делались и для организмов животных. Морфологи первой половины XIX века строили идеальный архетип позвоночного животного. Вот пример из книги Роберта Оуена (рис.7)[19]:

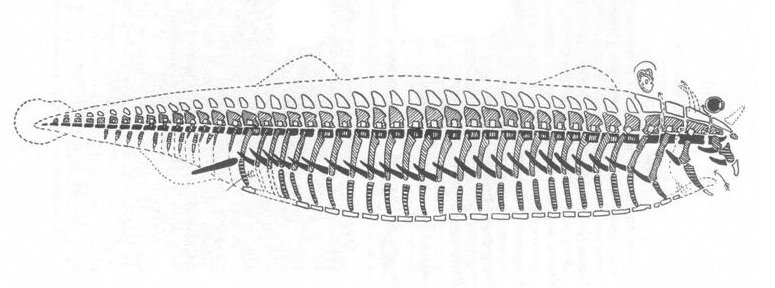  Рис. 7

Занимающий в скелете центральное место позвоночник обладает явной (скажем, для математика) способностью развиваться в направлении хвоста сколь угодно далеко[20], и опять, как и для растения, реальные позвонки становятся все меньше по мере приближения к концевой точке[21].

VI. Выводы. Обратимся еще раз к богословию. Представление об умопостигаемом, сверхчувственном пространстве, о Небесах единого дня Творения является неотъемлемой частью православного представления о тварном мире. Можно предположить, что такое пространство содержит идеальные прообразы (эйдосыплатонизма, в православии имеется учение  о логосах,принадлежащее преп. Максиму Исповеднику) реальных физических (и не только) предметов и структур нашего мира. И представление о существовании такого пространства отнюдь не противоречит современной науке, хотя и не разработано в ней в должной мере.

Первый пример: числа, прямые, треугольники и иные математические предметы. Их нет в окружающем нас мире, и наука (в данном – случае математика) использует их именно как идеальные предметы. Философский платонизм полагает их существование в особом мире или пространстве идей.

Второй пример. Равномерное прямолинейное движение по бесконечной (!) прямой, введенное в физику Галилеем. Именно введенное adhoc , а не выведенное из каких-то эмпирических наблюдений. В окружающем нас пространстве таких движений просто нет.

Можно сказать, что идеальные конструкции пронизывают науку и являются наряду с эмпирическими наблюдениями (вспомним телескоп того же Галилея) одними из наиболее эффективных средств ее развития.

Переходя теперь к вопросу о существовании Бесконечности, можно сказать, что она находится в идеальном мире, а в чувственном мире есть ее конечная реализация. Тогда можно сделать вывод и о существовании бесконечной иерархии часов и сопряженных циклов. Она существует в таком идеальном пространстве, а земная жизнь лишь стремится ее реализовать, не имея, впрочем, возможности достигнуть своего бесконечного предела.

Возможное применение этого круга идей в естествознании (и, может быть, в изучении социума) состояло бы в построении аксиоматической теории идеальной системы циклов (наподобие предложенной нами аксиоматической системы для времени).

Позволим себе указать на возможное значение такой теории для разрешения вопроса, весьма волнующего в последнее время верующих (и не только) научных людей. Речь идет о спорах креационизма и эволюционизма о происхождении жизни и всего многообразия живых организмов. Мы не говорим здесь о механизмах эволюции: т.н. синтетическая теория эволюции (которая, как еще недавно считалось, отвечает на все вопросы эволюционного развития), кажется, сильно покачнулась, если и не совсем повергнута[22]. Речь пойдет о самом факте существования эволюции. По нашему мнению, именно признание факта постепенной направленной эволюции кардинально противоречит православному представлению о возникновении мира.

Думается, что разрешение этого противоречия возможно лишь на пути принципиальных изменений наших представлений о времени, отказе от единой линейной направленной шкалы, переходе к представлению о системе многих независимых линейных времен[23]. Тогда каждый живой организм должен существовать в своем времени и нет абсолютного критерия, позволяющего соотнести, соупорядочить события жизни одного организма с событиями жизни другого. В каждом отдельном случае такое отношение (порядок событий, кто раньше, кто позже) должно устанавливаться самостоятельно и независимо. Пожалуй, единственным возможным основанием такого соответствия является факт встречи двух организмов, их общения друг с другом.

Изложенные выше соображения о системе природных и жизненных циклов приводят к предположению о существовании универсальной экологической системы, которая определяет развитие живых существ во времени. Такая (бесконечная!) система циклов должна быть «всегда», в вечности.

Роль системы сопряженных биогеохимических циклов в существовании биосферы (и геосферы – с учетом космических факторов) постоянно подчеркивает в своих работах Г.А.Заварзин[24]. Это, по его словам, «основная биосферная машина планеты». В этой системе имеется постоянно «бактериальная система, катализирующая химические превращения в сопряженных биогеохимических циклах. К ней не добавилось ничего принципиально нового за время эволюции. Все последующие формы жизни вписывались в эту систему, не меняя ее принципиально».

Также[25] он указывает, что «новый организм может установить себя только в том случае, если он соответствует существующему сообществу. Если он не соответствует этому сообществу, он просто в него вписаться не может <…>. Отсюда следует, что старое должно быть сохранено как необходимое предварительное условие для устойчивого существования нового. По большой шкале эволюция происходит не путем замены, но аддитивно[26], поскольку новые члены выживают только в том случае, если они соответствуют существующим сообществам».

Итак, для того чтобы геосферно-биосферная система работала, обязательно должна иметься система сопряженных циклов, охватывающая ее сверху донизу. Но если признать наличие вечного идеального мира и существующей в нем универсальной системы циклов, которая реализуется в конечной системе циклов нашего мира, каждого со своим временем, то может появиться новый взгляд на эволюцию, имеющий весьма нетривиальный и точный смысл.

ПРИЛОЖЕНИЕ I (к аксиоматике часов)

Назовем часами одномерную компактную группу Ли, снабженную инвариантной относительно сдвигов метрикой. Такая группа будет метризованной окружностью S с выделенной точкой (нулем) s₀ . Период l = l(S) – это длина окружности S .  Будем обозначать через S_l окружность длины l .

(Непосредственная) синхронизация часов – это сюръективный гомоморфизм групп Ли, являющийся локально изометрией. Иначе говоря, это конечное накрытие окружностей f: S’ → S , сохраняющее локально метрику и также отмеченные точки f(s’₀) = s₀ . Синхронизация (в общем случае) между окружностями (часами) S и S ’ представляет пару отображений f: S → S’’ и f’ : S’ → S’’ , являющихся непосредственными синхронизациями с третьей окружностью S’ ’. Имеем тогда для периодов часов:

l(S) = deg (f) l(S’’),l(S’) =deg (f’) l(S’’) и l(S) = deg (f)/deg (f’) l(S’).

Последовательность окружностей, которая рассмотрена в основном тексте, имела вид S₂ⁿ, где n = 0, 1, 2,… Там был выбран такой закон роста периода лишь для простоты. Пусть, более общо, имеем S_n, n = 0, 1, 2, …

и отношения синхронизации выглядят так:

f_mn : S_m → S_n, если n делит m.

Универсальное время представляет собой (проективный) предел такой системы часов. В предположении наших аксиом вся система часов сводится к этой конкретной системе, и предел по всем возможным часам будет равен пределу по такой последовательности часов[27]. Набор { S_n, f_mn } представляет собой проективную систему групп (наделенных метрикой).

Если R – прямая с евклидовой метрикой и фиксированной нулевой точкой, то   R – группа вещественных чисел по сложению, и имеем канонический изоморфизм метризованных групп

R /n Z → S_n,

где Z – группа целых чисел.

Тогда проективная система может быть записана так:

S_m     →      S_n → … →   S₁

║               ║                      ║

R /m Z → R /n Z → … → R / Z .

Переходя к проективному пределу в верхней строке этой диаграммы, получаем:

lim_n S_n → … S_m →   S_n   → … →    S₁

    ↑                  ║        ║              ║

R → …R /m Z → R /n Z → … → R / Z ,

где левое вертикальное отображение является вложением ньютоновской прямой R в универсальное время. Вычислим, как устроено последнее.

Пусть A _f= Π ’_p Q _p – группа конечных аделей, где Q_p – аддитивные группы p– адических чисел, а p = 2, 3, 5, … пробегает все простые числа. По определению, A _f= {(f_p) :  f_p принадлежит Q _p& f_p принадлежит Z_p для почти всех p }, где Z_p – группы целых p -адических чисел. Она содержит компактную подгруппу Z ^ = Π_p Z_p, произведение всех групп Z_p[28]. Поле Q рациональных чисел вкладывается в полную группу аделей A = A _f+ R в качестве дискретной диагональной подгруппы (используя естественные вложения Q в Q _p и Q в R ). Фактор-группа A / Q компактна.

В силу теоремы о сильной аппроксимации имеем:

A = Z ^ + Q + R

и тогда:

A / Q = ( Z ^ + Q + R )/ Q = ( Z ^ + R )/( Q ∩( Z ^ + R )) = ( Z ^ + R )/ Z .

Отсюда получаем точную последовательность:

0 → Z ^ → A / Q → R / Z → 0

и более общо:

0 → n Z ^ → A / Q → R / n Z → 0,

для любого n = 1, 2, … Переходя к пределу, получаем окончательный ответ:

 lim_n S_n =lim_n R /n Z = A/Q .

Из приведенных выше вычислений сразу вытекает, что имеется точная последовательность:

0 → R → A / Q → Z ^/ Z → 0.

Сдвиги прямых R покрывают весь предел, т.е. группу A / Q, и этих прямых столько, сколько элементов в группе Z ^/ Z . Поскольку группа Z всюду плотна в Z ^, находим, что сдвинутые прямые, в том числе и R , всюду плотны в группе A / Q , которая и есть наше универсальное время.

Еще одна неожиданная особенность универсального времени состоит в том, что, как множество, оно компактно. Можно сказать, что все имеющиеся в нем прямые образуют тугой клубок, где каждая прямая подходит сколь угодно близко к каждой точке этого клубка, т.е. к каждой точке любой другой прямой.

ПРИЛОЖЕНИЕ II (к аксиоматике циклов)

В этом приложении мы дадим математическую формулировку свойств циклов, приведенную в основном тексте, и обсудим возможности построения аксиоматики системы циклов, развивающую аксиоматику системы часов. Мы начнем с формулировки, которая приближена к имеющимся теориям переноса в механике непрерывных сред. Положим в основу неопределяемое понятие цикла. Цикл состоит из часов и переноса какого-то вещества. Будем считать, что количество вещества измеряется действительными числами. Тогда цикл задается временем t часов с каким-то периодом T и функцией I(t) = количество вещества, переносимого в момент времени t. Время t принадлежит окружности S, связанной с часами.

Имеем тогда следующие свойства замкнутого изолированного цикла:

1. I : S → R,т.е.  I(t + T) = I(t).
2. Для любых t, t’ из S  I(t) = I(t’).
   

Более интересен случай нескольких взаимодействующих циклов. Возьмем для простоты два цикла (обобщение на случай n циклов с любым n получается очевидным образом). Пусть эти циклы суть (t₁, I₁) и (t₂, I₂).

К этим данным нужно добавить функции I₁₂ и  I₂₁, представляющие количество вещества, переносимого в какой-то момент времени от первого цикла ко второму и обратно. Вообще говоря, I₁₂ и  I₂₁  различны.

Тогда имеем следующий список свойств:

1. Часы  t₁ и t₂ синхронизированы, т.е. времена t₁ и t₂ выражаются как целочисленные кратные некоторого единого времени t.
2. I₁(t₁ + T₁) = I₁(t₁),

          I₂(t₂ + T₂) = I₂(t₂).

3. Для любых двух моментов t, t’ единого времени 

          I₁(t) +  I₂(t) = I₁(t’) +  I₂(t’).

4. В едином времени

          dI₁/dt  =  I₂₁(t)  -  I₁₂(t)

          dI₂/dt  =  I₁₂(t)  -  I₂₁(t).

Приведенный список свойств конечно же отвечает многим реальным циклам, но далеко не всем. Во многих системах циклов участвует не одно, но несколько веществ и, что более существенно, между этими веществами происходят химические (или иные) реакции. См. приведенные выше примеры.

В такой ситуации более естественно измерять количество вещества в молях, как это принято в химии и учитывать стехиометрические соотношения между ними. Можно даже предложить считать число молекул, переносимых в единицу времени в цикле или между циклами. Тогда «непрерывная» функция I(t) должна быть замененена на «дискретную» функцию N(t), принимающую значения не в R, а в множестве N натуральных чисел. Для нее можно написать похожий список свойств. Можно даже объединить эти свойства, считая, что функции I(t) где-то непрерывны, а где-то дискретны. Техника теории меры в математическом анализе позволяет сделать это без труда.

Если рассматривать дискретную ситуацию, то возникает вопрос о выборе «правильной» метрики в множестве N. Обычная для современной науки евклидова метрика в R определяет метрику такого же типа (как говорят архимедову, т.е. удовлетворяющую аксиоме Архимеда) в N. Но в N имеется еще бесконечно много неархимедовых метрик, зависящих от выбора простого числа p = 2, 3, 5, … Пополняя N  по этим метрикам, мы получаем поля p-адических чисел, которые у нас возникали в предыдущем приложении.

Мы думаем, что метрика такого типа более адекватна изучению химических реакций, где соотношения делимости целых чисел (типа закона Дальтона) играют фундаментальную роль[29]. Эта метрика должна быть основной на уровне отдельных молекул, а евклидова метрика становится значимой для больших весовых количеств рассматриваемого вещества.

Последнее замечание состоит в том, что данный выше набросок носит очевидно феноменологический характер, не проникая в глубь явления. Этим он резко отличается от обсужденной раньше аксиоматики часов, которая, как мы считаем, носит онтологический характер. Тем не менее, в какой-то форме эти свойства могут войти в будущую аксиоматику систем циклов, находящуюся на том же уровне, что и аксиоматика часов[30].